In this post, we are going to learn an important concept in photochemistry—spin multiplicity. This concept plays a critical role in understanding how molecules behave when they absorb light and transition between different energy states.
Understanding spin multiplicity is essential for explaining:
- Why some transitions are allowed while others are “forbidden”
- Why phosphorescence is slower than fluorescence
- How intersystem crossing (ISC) works
As we dive deeper into this topic, you’ll see how spin states govern the photochemical behaviour of molecules—from their reactivity to their emission properties.
Spin Multiiplicity
In photochemistry, when a molecule absorbs a photon, it is promoted from its ground electronic state to an excited state. But not all excited states are the same—some are singlets, while others are triplets, and this distinction arises due to the arrangement and spin of electrons.
Spin multiplicity refers to the number of possible orientations of the total spin of a molecule. It is defined as:
Spin multiplicity = 2S+1,
where S = the total spin quantum number
The total spin quantum number (S) is calculated by adding the spins of all unpaired electrons.
Spin multiplicity is a mathematically defined term and, as such, cannot be proved by experimentation. Think of spin multiplicity like the concept of a triangle in geometry. A triangle is defined as a shape with 3 sides. You don’t prove it experimentally — it’s true by definition. You can observe shapes in the world that match the definition of a triangle and confirm your models of geometry apply well to the real world.
So basically, the spin multiplicity tells us how many spin states a molecule can have (due to unpaired electrons). It also gives us information about the magnetic behaviour and photochemical transitions.
Now that we have understood what this term means, let us try to understand it in a better light. We know that most molecules have an even number of electrons in the ground state. All these electrons are spin paired (↑↓). Spin pairing refers to two electrons occupying the same atomic or molecular orbital with opposite spins (one +½, one –½). Spin pairing helps to stabilise the molecule.
How Does Spin Pairing Stabilise a Molecule?
- Lower Energy Configuration:
- When two electrons are spin-paired in a bonding orbital, they form a stable electron pair. This lowers the overall energy of the system.
- Minimised Electron Repulsion:
- Opposite-spin electrons in the same orbital are closer together but experience less repulsion due to their opposing magnetic moments.
- This allows them to stay in a low-energy, stable configuration.
Singlet and Triplet States
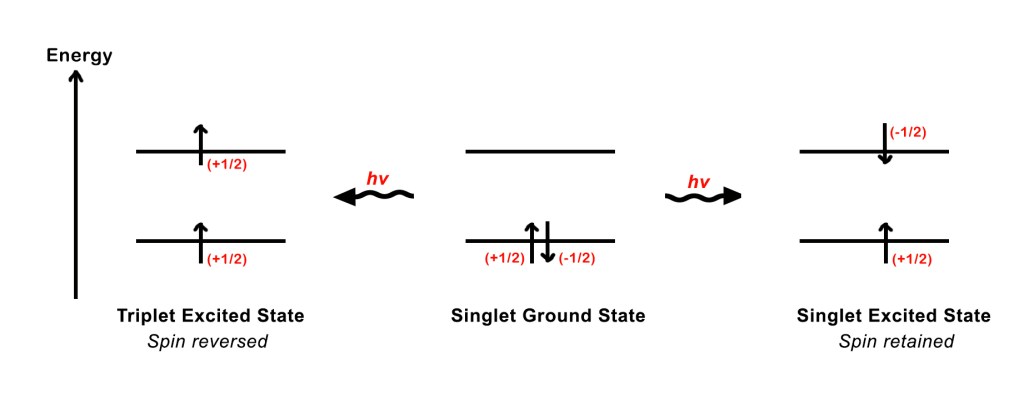
In the ground state, the upward orientation of the electron spin of one electron is cancelled by the downward orientation of the spin of the other electron. Thus, the net spin is zero.
S1 = +1/2 , S2 = -1/2, then
The total spin S= S1 + S2 = 1/2 -1/2 = 0.
Hence, the spin multiplicity = 2S+1 = 2(0)+1 = 1. This is referred to as the singlet ground state.
When a photon of suitable energy is absorbed, one of the paired electrons jumps to a higher energy level, i.e it gets excited. Excitation can occur in two ways –
i) The excited electron can retain its original spin – the spins of the electron in the ground state and the excited state are anti-parallel (↑↓) . In this case, the net spin is zero and the spin multiplicity = 2S + 1 = 1. Thus, we say that the molecule is in the singlet excited state.
ii) The excited electron can reverse its spin – the spins of the electrons in the ground and excited states are parallel (↑↑). In this case, the molecule has a net spin, S = +1/2 +1/2 = 1.
and the spin multiplicity = 2S + 1 =2(1)+1= 3. Thus, we say that the molecule is in the triplet excited state.
For one-electron atoms, only doublet states are possible; for two-electron atoms, singlet and triplet states arise; for three-electron atoms, doublets and quartets can occur; for four-electron atoms singlet, triplet and quintet states are generated and so on. Odd number of electrons give rise to even multiplicity, whereas even number of electrons give rise to odd multiplicity.
| Number of Unpaired Electrons | S Value | Spin Multiplicity | Type of State |
|---|---|---|---|
| 0 | 0 | 1 | Singlet |
| 1 | 1/2 | 2 | Doublet |
| 2 | 1 | 3 | Triplet |
| 3 | 3/2 | 4 | Quartet |
We will continue our discussion on this topic in the next post too… Till then,
Be a perpetual student of life and keep learning…
Good day!
Madoverchemistry 