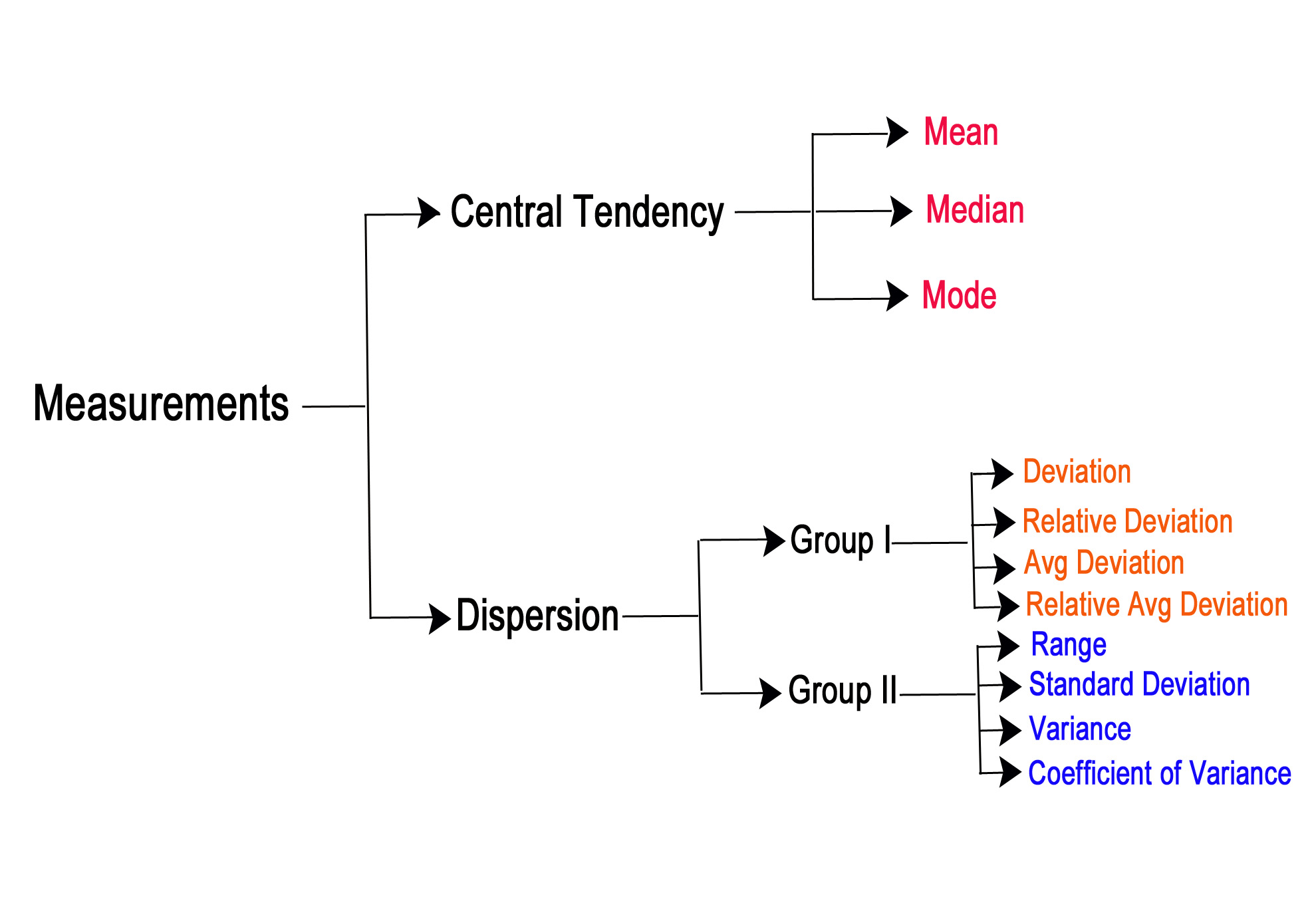
We have been exploring the concepts of ‘measurements’ in the previous few posts. We can summarize these concepts as follows-
When we measure entities, we might encounter numbers with decimal points. Sometimes the numbers have more digits after the decimal point (e.g.- 0.89657). In such cases, we are expected to round off the numbers to get a simpler number. However, the rounding off is NOT done arbitrarily. There are specific rules to carry out this process.
While rounding off we retain the numbers which are important and round off the numbers which yield less information. Together the important numbers and the rounded off digits are referred to as ‘SIGNIFICANT FIGURES’. In this post, we shall start studying the rules of rounding off and getting significant figures.
Significant Figures/Numbers
The concept of significant numbers is ubiquitous to all calculations made in scientific studies. So what are significant numbers?
Significant figures are the digits that are exactly known (certain) and the first uncertain digit.
e.g. Consider a value of 0.00900 kg.
How many significant figures does this value have?
If we rewrite this value in ‘grams’, we get a value of 9.00g. So, the three zeros before the digit ‘9’ are insignificant as they lose their significance when the quantity is expressed in grams. Note that, 0.00900kg = 9.00g. So, essentially both the quantities are the same. However, the units are different. Thus, in the above example, we have only 3 significant figures namely – 9,0,0.
WHAT DO SIGNIFICANT FIGURES TELL US?
Significant numbers are the digits which tell us how accurate and precise our measurement is.
e.g. Consider the same value again – 9g. This value can be written as 9g or 9.00g.
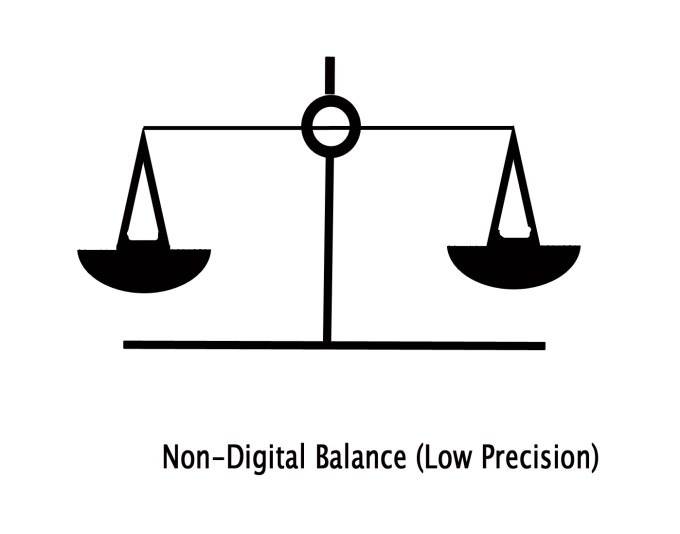
If only ‘9g’ is mentioned, one is unsure about how precisely the measurements were done. This is because only one significant digit is given. A simple, non-digital balance would give us such a rough result. Technically, the weight could not be exactly 9g but somewhere close to it. The weight could be 9.02 or 9.04 or any other value close to 9g.Thus, 9g ⇒ rough measurement ⇒ Weight measured by a simple, non-didgital balance ⇒ Low Precision.

Whereas, when we write 9.00g , we indicate that the measurement done was more accurately (upto two digits after the decimal point). Here three significant figures are stated. So one can be sure that the weight is exact 9.00g. Such accuracy is obtained by a digital balance. So the last two zeros indicate accuracy and thus are significant along with the non-zero number ‘9’. Thus,9.00g ⇒ more exact measurement ⇒ weighed by digital balance ⇒ High precision.
Thus, when a number is rounded, the number of significant figures is known as the precision of the number. More the number of significant figures, more is the precision.
Rules for calculating significant figures
(Significant figures are highlighted in orange colour)
- All non-zero digits (1 to 9) and zeros in between non-zero digits are considered significant.
e.g. 0.78902 has five significant figures. - Zeros that appear immediately before and after the decimal point are called leading zeros. Leading zeros are NOT significant.
e.g. 0.00867 has three significant digits. The zero before the decimal and the two zeros just after the decimal point are NOT significant numbers.
- Zeros that appear after the last non-zero digits are called trailing zeros. There are two possibilities for such zeros –
Case I – For a number with a decimal point, these trailing zeros are significant. e.g. 0.2300
Case II – For a number without a decimal point, the trailing zeros may or may not be significant. This is a case of ambiguity and one cannot determine the significance of the zeros correctly.
e.g. Distance between two cities is 1830 km. Predicting whether this distance was accurately measured or not is not possible in this case. The distance could just be mentioned as a round figure. - Rounding the digits –
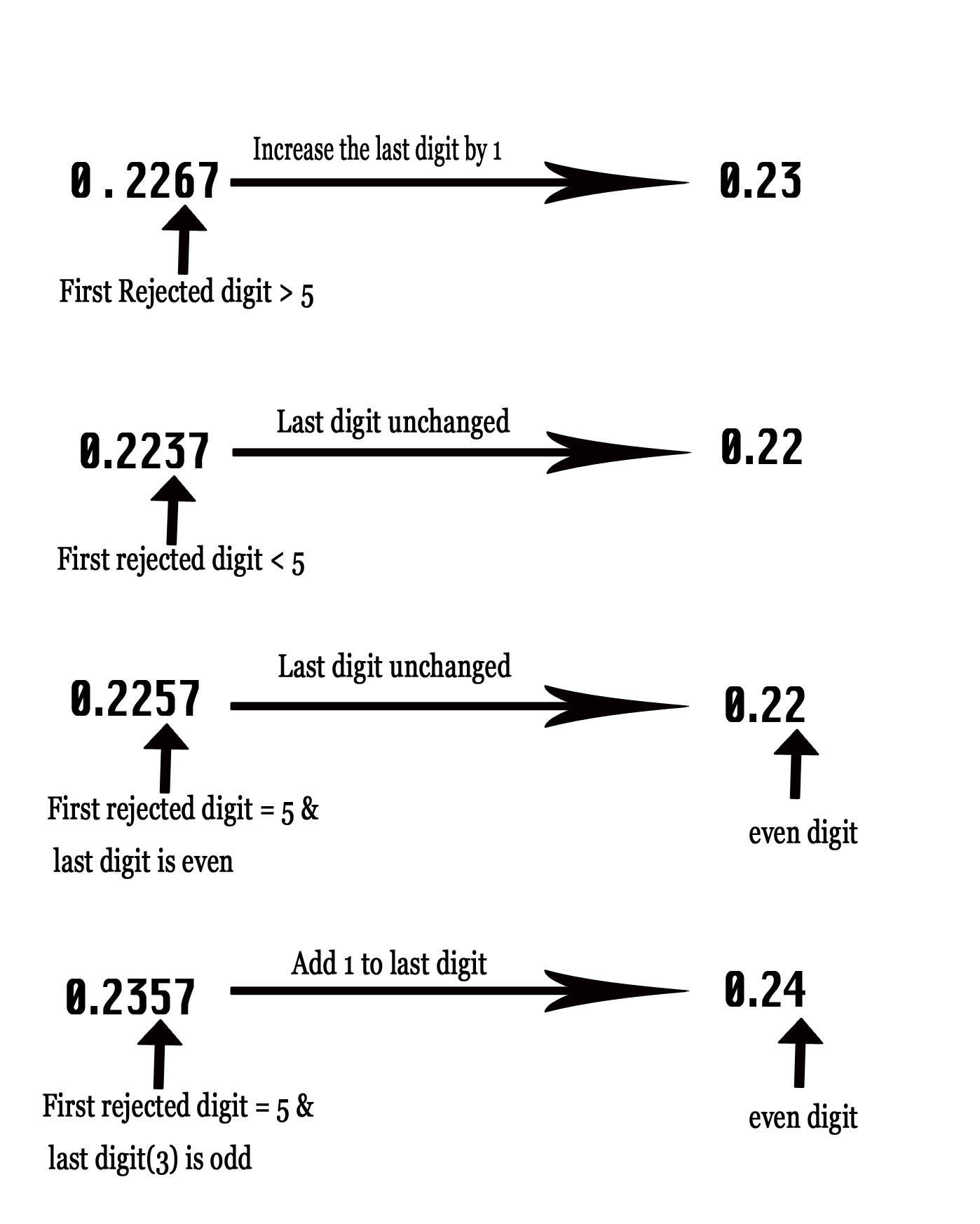
RULE I – If the first rejected digit > 5 ⇒ increase the last significant digit by one.
RULE II – If the first rejected digit <5 ⇒ keep the last significant digit unchanged.
RULE III -If the first rejected digit = 5 ⇒ Round so that the result ends with an even number. Thus, if the previous digit is even we keep the it unaltered and if its odd , we add one to it to make it an even number.
When rounding off the digits, one has to specify how many significant figures are needed.
Consider the number 0.2267. If we want to write this number with two significant figures, then first we have to ignore the leading zero which is just before the decimal point. Now we are left with 4 digits namely 2,2,7, and 7. We have to convert these 4 digits to two. So the third and fourth digit needs to be rejected. In the above number 6 is the first rejected digit. This value of this digit is more than 5. Thus, RULE I applies. We increase the previous digit by 1 and then reject the last two digits of this number. Thus, now the value would be 0.23 with two significant figures. Refer to the following figure for more examples.

- Addition & Subtraction – Retain only as many decimals in the final result as those in the number with fewest decimals.
e.g. 14.22+8.145 +120.4 = 142.765. Here, the number with the fewest decimals is 120.4 (only one place after decimal point).Therefore, we will round the answer to have only one digit after decimal point. Thus, the answer is 142.8 - Multiplication & Division – Retain only as many significant figures as those in the number with the fewest significant figures.
e.g. (25×0.524)÷100 =0.131. Here,
25 → 2 significant figures.
0.524 → 3 significant figures.
100 → 3 significant figures. Thus, the number with the fewest significant figures is 25. So the answer can have only two significant figures.Thus, our answer is 0.13.
Though these topics seem very unexciting, they have wide application in science. Their importance can only be understood in the light of high-precision work. We shall continue our discussion on significant numbers in our next post too. Till then,
Be a perpetual student of life and keep learning…
Good Day!
One comment