69.Covalent Bonding(15)- More concepts in hybridization theory(2).

Molecules with hybrid orbitals can be of two types –

A] Symmetric molecules where all bonds are the same.
e.g.- CH4 molecule, where all bonds are C-H bonds. So, in this type of molecule, all substituents on the central atom are the same. This type of molecule show ideal bond angles and bond lengths as predicted by the VSEPR model.

B] Asymmetric molecules, where all the substituents on the central atom are not the same.
e.g.- NH₃ molecule, where nitrogen is bonded to three hydrogen atoms and has a lone pair too.
OR
Water molecule with two lone pairs of electrons has sp³ hybridized oxygen atom.

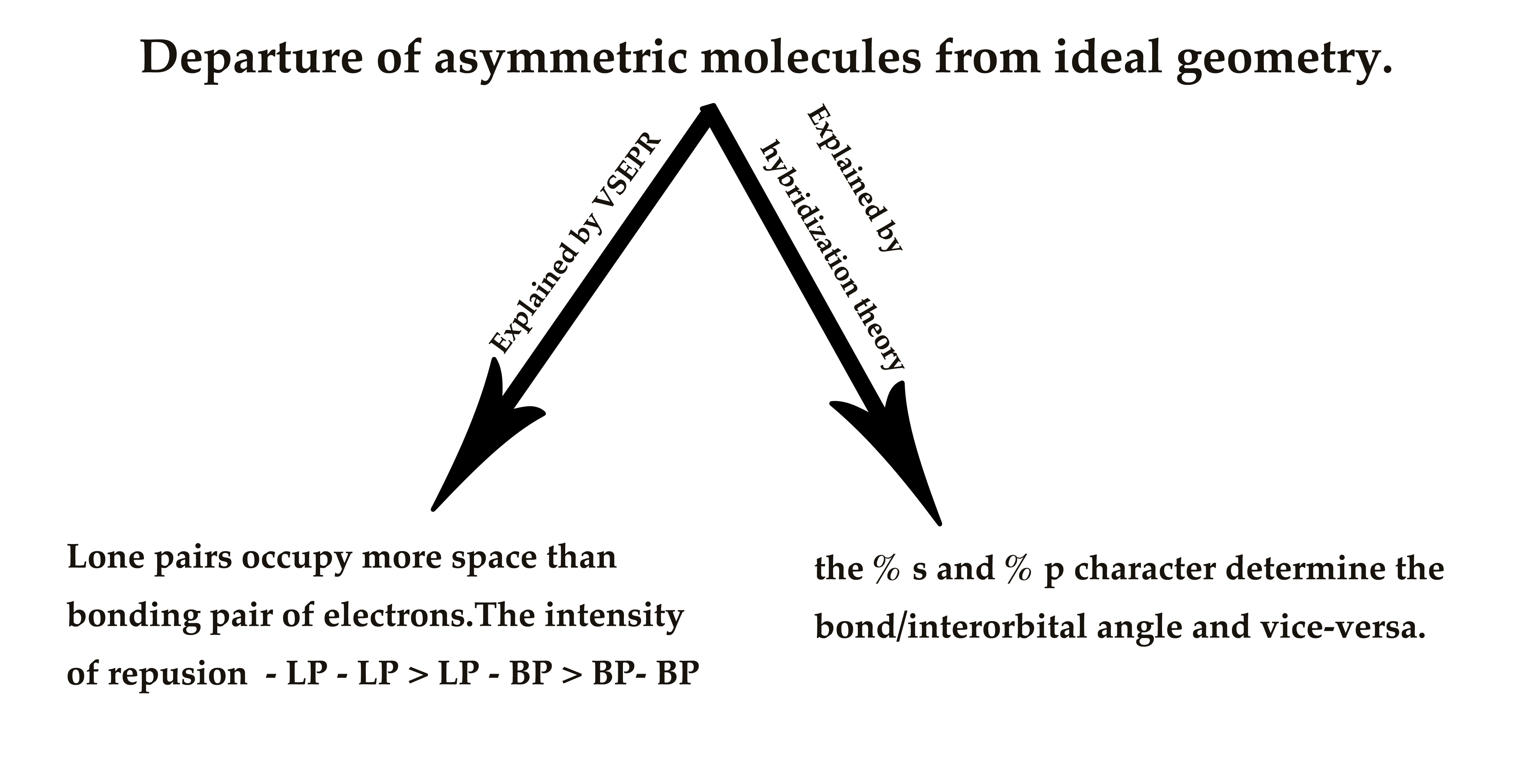
Asymmetric molecules show the departure from ideal behavior, as predicted by VSEPR.

We have already studied,  how the VSEPR theory, explains this departure from ideal bond angles and bond lengths. It does so, by stating that the lone electron pair occupies more space than the bonding pair of electrons. However, hybridization theory explains the same non-ideal behavior in a different way. Hybridization theory relates the %s and % p character to bond angles.

Let us study in detail how the %s character and bond angles are related.

---

From the last post we already know,

i= f_p / f_s , where,
i ⇒hybridization index.
f_p ⇒ fraction of p character.
f_s ⇒ fraction of s character.

For hybrid orbitals containing s and p orbitals, the sum of f values for all the hybrids on a given atom must be equal to 1.

∴f_s +f_p = 1

e.g.- In sp³ hybridization, f_s +f_p= 0.25+0.75= 1

---

For all hybridization, s =1, as there is only one valence s orbital, which takes part in the mixing process.

We also know that the total no of hybrid orbitals formed = i + 1

∴f_s= 1 / (i + 1)  and f_p= i/(i+1) → (eqⁿ 1)

Applying the above formula to sp³ hybridization , i= 3 .So,

f_s= 1 / (3 + 1) = 1/4 = 0.25
f_p= 3 / (3 + 1) = 3/4 = 0.75

According to hybridization theory, the % s and % p character determine the bond/interorbital angle (i.e the angle between two hybrid orbitals ) and vice-versa.

When we plot the f values vs the interorbital angle (θ), we get the following graph –

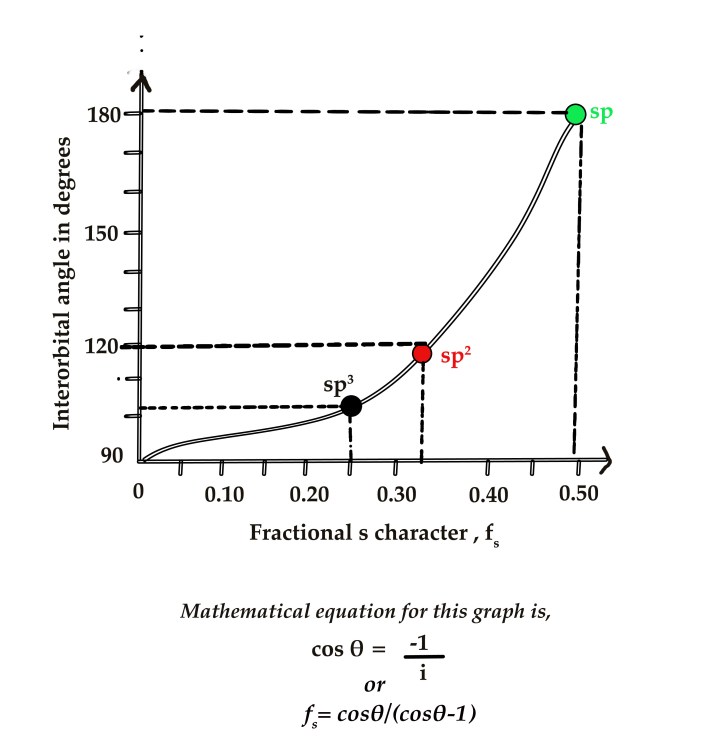
As seen in the above graph ,
for sp³ hybridization ,  i=3 , f_s = 0.25 (i.e 25% s character) , and θ _sp3 = 109.5 º 
for sp² hybridization , i=2,  f_s = 0.33 (i.e 33% s character) and θ _sp2 = 120 º &
for sp hybridization , i=1,  f_s = 0.50 (i.e 50% s character) and θ _sp = 180 º.

The above graph yields the relation,
cos θ = -1 / i   or f_s=cosθ/(cosθ-1) – This is a mathematical representation of the graph, which is beyond our course of study. So, we shall just take the formula as it is. 

Let us check,  if the above equation, cos θ = -1 / i   gives us the correct values of θ.

i) For sp³ hybridization ,  i=3 , cos θ = -1 / i .
∴cos θ = -1 /3
θ = cos^-1 ( -1/3) = 109.5º 

ii)For sp² hybridization ,  i=2 
∴cos θ = -1 /2
θ = cos^-1 ( -1/2) = 120º 

iii)For sp hybridization ,  i=1 
∴cos θ = -1 /1=  -1
θ = cos^-1 (-1) = 180º 

It’s just amazing to see how mathematics, theoretically proves, the observations made experimentally !

---

 Relating  f_s to θ 

The bond angle (θ) is related to f_s value by the following two equations  – 

 f_s=cosθ/(cosθ-1) or  cosθ = f_s/ f_s-1

---

Also, the summation of all f_s values for a given atom should equal to one, as only one atomic s- orbital is involved in the hybridization process.

∴∑ f_s = 1.

Consider methane molecule(CH4). In this molecule, the central carbon atom is sp³ hybridized. It has 4 hybrid orbitals. Each sp³ hybrid orbital will have f(s)=0.25. However, carbon has 4 such orbitals.Thus, for the atom,

∑f(s) =0.25+0.25+0.25+0.25= 1.

Remember the entire s-orbital is used to make hybrid orbitals.

We continue this discussion in the next post as well. Till then,

Be a perpetual student of life and keep learning ..

Good Day!

References and Further Reading –

1.http://www.acadblock.com/inorganic-chemistry/inorganic-comprehension-ft64/
2. Organic Chemistry by Roger Macomber, Volume 1.