We concluded the last post by stating that molecules are anharmonic oscillators. In an anharmonic oscillator, the restoring force(F) is no longer proportional to the displacement(x). Thus, the graph of the potential energy against the displacement is NOT a perfect parabolic curve. The curve is slightly distorted as shown below-
To explain the vibrational interaction between two atoms in a diatomic molecule, we need a concept termed ‘The Morse potential‘.
The Morse Potential
- Morse potential is used to describe the anharmonic oscillator model in molecules.
- The potential between two atoms in a real molecule is NOT symmetrical.Thus, molecules behave as anharmonic oscillators.
- The Morse diagram correctly depicts the behaviour of molecules and helps to calculate the bond energy correctly.
- The difference between the graphs of harmonic (black color) and Morse potential (green color) is shown below-
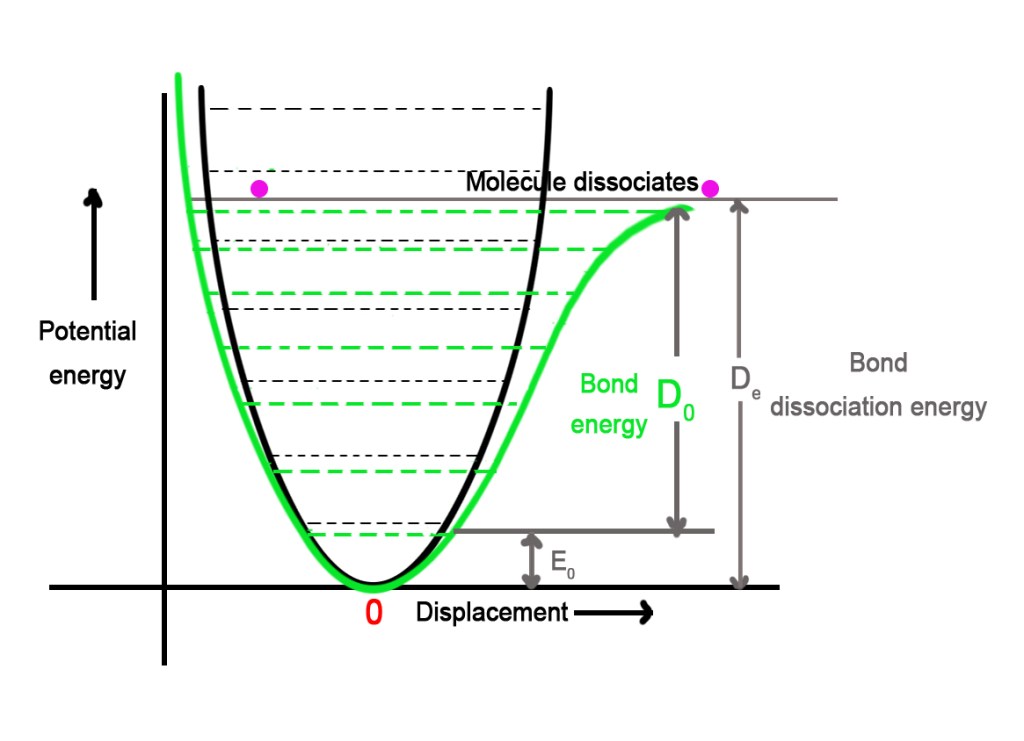
As seen in the figure above, for the lower energy states, the harmonic and the Morse potential curves are quite similar. However, when we move to higher vibrational states, the curve starts shifting to the right gradually. The higher energy states show this shift to a greater extent.
- Note that the spacing between two successive vibrational levels in the Morse diagram decreases as one approaches the dissociation energy.
- The threshold where the bond breaks is different too. The Morse diagram shows us that the molecule breaks at much lower energy than predicted by a harmonic oscillator model.
In the last post 173, we discussed that the bond dissociation energy is the energy required to break the bond between two atoms. We started calculating this energy from the zero-point energy till the point where the bond ruptured. The Morse diagram correctly shows that this calculation is not correct too.
The bond dissociation energy is different than the ‘bond energy’.The bond energy is calculated from the first vibrational energy level v”=0 and NOT FROM THE ZERO-POINT ENERGY, which is slightly above the bottom of the potential well (see the figure above).
Why is the energy not calculated from the zero point level?
We know that zero-point energy is the energy of the molecule at equilibrium- when the molecule is still. However, in reality, molecules are never completely still. They are in a constant state of vibrations (except at extremely low temperatures). Thus, it becomes necessary to subtract the zero-point energy (E0), to get the true value of bond energy(D0).
∴ Bond energy (De) = Bond dissociation energy (D0) – Zero-point energy (E0)
Thus, THE ENERGY REQUIRED TO BREAK THE BOND IN A MOLECULE IS THE ‘BOND ENERGY‘ AND NOT THE BOND DISSOCIATION ENERGY.
In the next post, we continue to discuss Morse’s potential in more detail.Till then,
Be a perpetual student of life and keep learning…
Good day!
References and further watching –
1)https://www.youtube.com/watch?v=UpGi4Yckry8