118.Aromaticity(11) – HMO treatment to benzene(2).

In the last post we saw how the HMO theory explains the aromaticity of benzene ring. In this post let us see how we get the energies of six MOs of benzene by applying this theory.

In the above figure we have labelled each carbon atom on benzene from 1 to 6. Applying the Huckel approximations, we can construct a matrix for benzene. Benzene has six p-orbitals (one on each carbon atom) and so we will have a 6×6 matrix. From post # 115 we know that –

Matrices in HMO theory , are tridiagonal matrices with α as the diagonal element and β as near diagonal element. There are two β’s at top right and bottom left as benzene is cyclic.

The Hamiltonian (H) matrix will be as follows –

When we solve the above matrix, we get the energy levels for various MOs in benzene. The matrices are solved by computers and thus even complex systems can be studied by HMO method. After solving the matrix, we get 4 different energy levels (there are 6 MOs)-

Two sets of degenerate energy levels  i.e MOs having the same energy ⇒

Set 1 – (Ψ_2,Ψ₃) or(π₂ ,π₃)  and
Set 2 –  (Ψ_4,Ψ₅) or (π^*₄ ,π*₅).

Two non-degenerate energy levels ⇒ Ψ₁ or π₁ , Ψ₆ or π*₆

NOTE – Here both ψ and π terms are used. The ψ terms are generally used during calculations and the π and π*  are notations used for representing the π MOs. Thus, ψ1 and π1 technically mean the same.

Representation of six MOs of benzene .

According to molecular orbital theory,

6 Atomic Orbitals(AOs) = 6 Molecular orbitals (MOs).

The six MOs can be represented as follows –

 

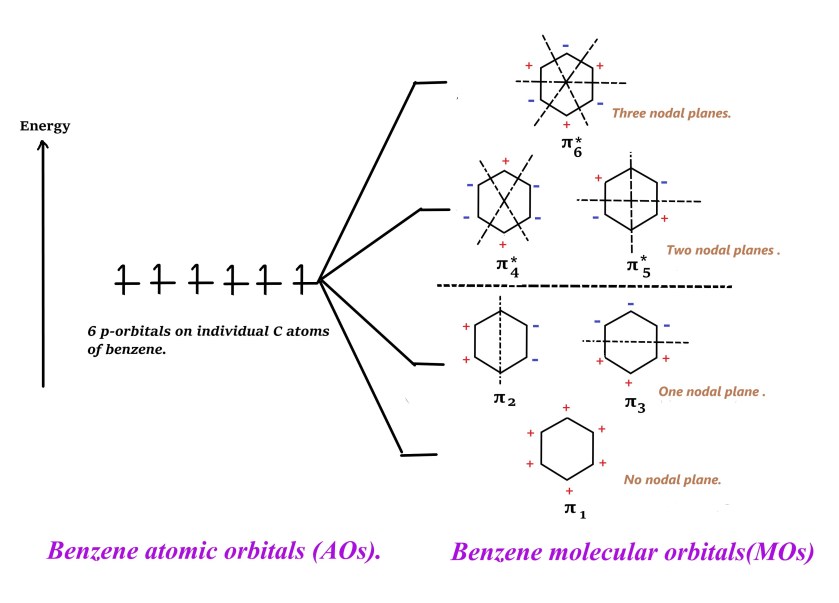
As seen in the above diagram , six atomic orbitals on individual carbon atoms of benzene linearly combine to form six molecular orbitals – three bonding (π₁, π₂ and π₃ )and three anti bonding (π₄, π₅ and π*₆ ).

The lowest energy MO ⇒ π₁ ⇒ has energy (α+ 2β) ⇒ has no nodes i.e there is no phase change. All positive lobes are on one side and all negative lobes of the p- orbitals on the other side.

π₂ and π₃  ⇒ energy (α-β) ⇒ one nodal plane i.e there is a phase change(from + lobe to – lobe) as shown below –

What does phase change exactly mean? We know that electrons behave as waves. When the sign is same (either + or -) , two electrons have their crests and troughs in the same phase.

π₄, π₅ are anti bonding degenerate orbitals ⇒ with energy (α-β) ⇒ two nodal planes, one passes through the bond (shown below) and one through atoms –

 

The π*₆ orbital has the highest energy as it has three nodal planes ⇒ energy (α-2β) –

 

In the next post we will compare benzene with another species using HMO theory.Till then,

Be a perpetual student of life and keep learning..

Good day !