73.Covalent Bonding(19)- Bent’s rule(2).

After having learned the statement of Bent’s rule in the earlier post, let us now study the rule with some examples.

We know that bond angle(θ) ∝ % s character (from post no 71). Then, according to Bent’s rule,

Now let us apply this to various examples and study Bent’s rule. 

Example 1 – Methyl Fluoride (CH₃F molecule).

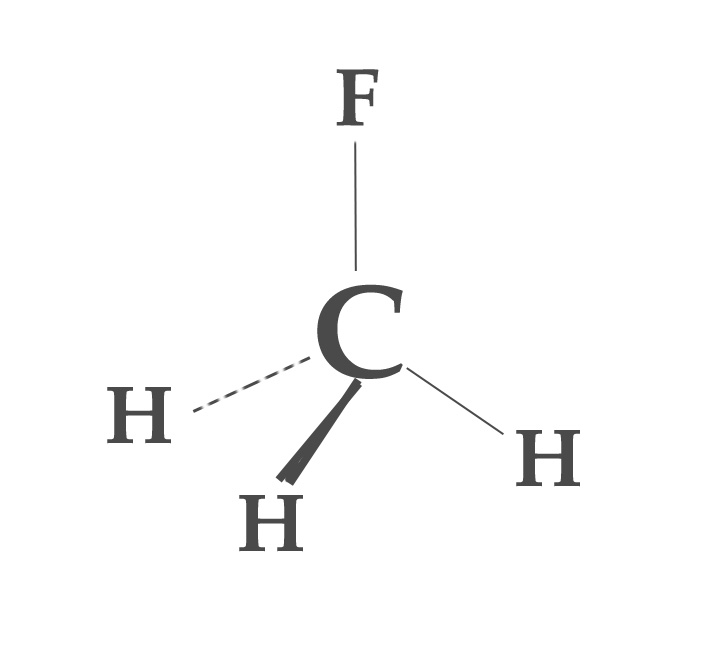
In a methyl fluoride molecule, fluorine is the most electronegative element. Just like methane (CH₄), this molecule is sp³ hybridized too. However, the distribution of s- character is not uniform in all the hybrid orbitals and so bond angles change too. This change is due to the presence of the F atom. We can predict this change in the bond angles using Bent’s rule.

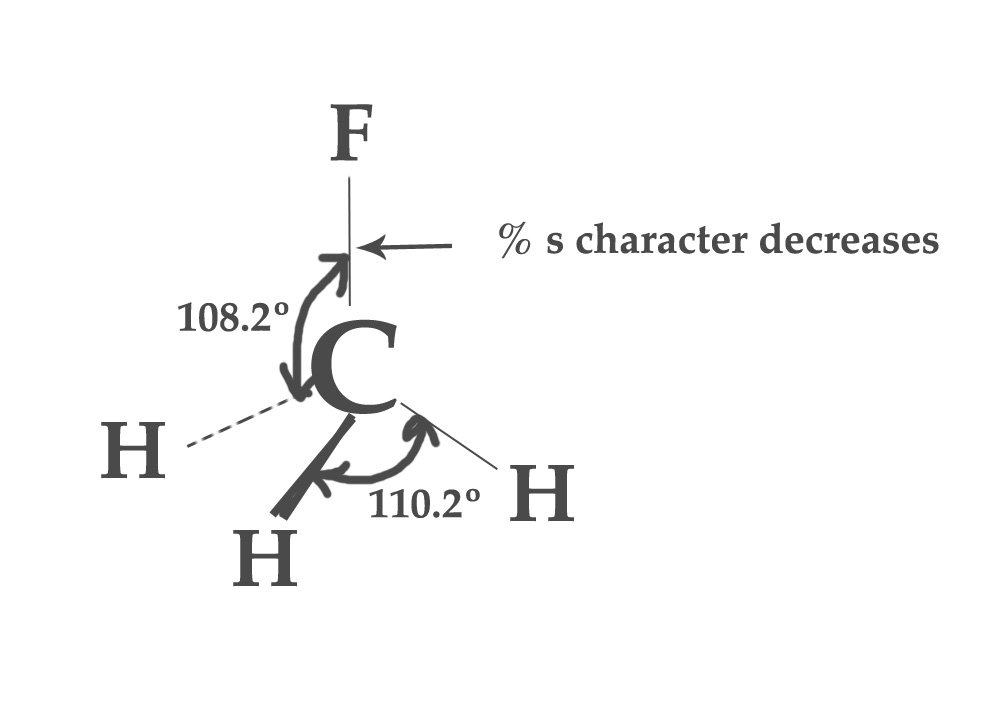
According to Bent’s rule, the orbital with less %s character will be directed towards the more electronegative element. Thus, obviously, the bond between C- F has less % s- character compared to C-H bonds. The bond angle will decrease too. Experimentally, the H-C-F bond angle is found to be 108.2º, which is less than 109.5º.

When the %s character in C- F bond decreases, it is accounted for by the increase in the  %s-character in the other three C-H bonds. So, C-H bonds have more %s character than expected, resulting in an increase in the bond angle between them. Experimentally, the H-C-H bond is found to be 110.2º.

Example 2 –  Sulphur tetrafluoride (SF₄).

We were skeptical about the structure of this molecule in the earlier post. Let us study its structure using Bent’s rule. SF4  is sp3d hybridized and has TBP geometry. There are four fluorine atoms and a lone pair in this molecule. As we know, according to the Pauling scale of electronegativity, fluorine is the most electronegative element in the periodic table (refer to post no 46). In the TBP geometry, there are three equatorial positions and two axial positions.

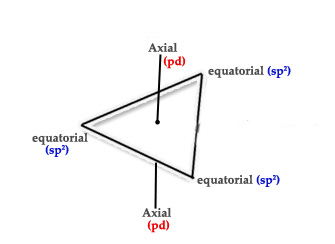
We can split sp³d as sp² + pd. 

As seen above, the sp² orbitals occupy the equatorial positions and the pd orbitals occupy the axial position. How can we be sure of this?  Let’s check whether this is true – 

Experimentally, we find out that the angle between equatorial substituents is 120º. We also know, 

i = – 1/ cosθ
∴i = – 1/ cos 120
i= –  1/ -(1/2) ..As cos 120 = -1/2
∴ i = 2
So, as the hybridization index is equal to 2 , the equatorial orbitals are sp² orbitals. 

Or we can use the formula from post 69 – f_s=cosθ/(cosθ-1) 

∴fraction of s- character in equatorial positions with θ = 120º is ,

f_s= cos(120) / (cos 120 -1)
= (-1/2) /(-1/2 -1)
=(-1/2)/ (-3/2)
= 1/3
=0.33.

 We know that it is sp² orbitals that have 33% s- character, so the equatorial hybrid orbitals are sp² hybridized.

Similarly, we know experimentally, that the angle with axial substituents is 90º. So, 

f_s=cosθ/(cosθ-1)
       = cos 90 / cos90 – 1
= 0/(0-1)
=0.

So, the amount of s- character in axial orbitals is zero i.e the pd part (no s character) occupies the axial position. Applying Bent’s rule – 

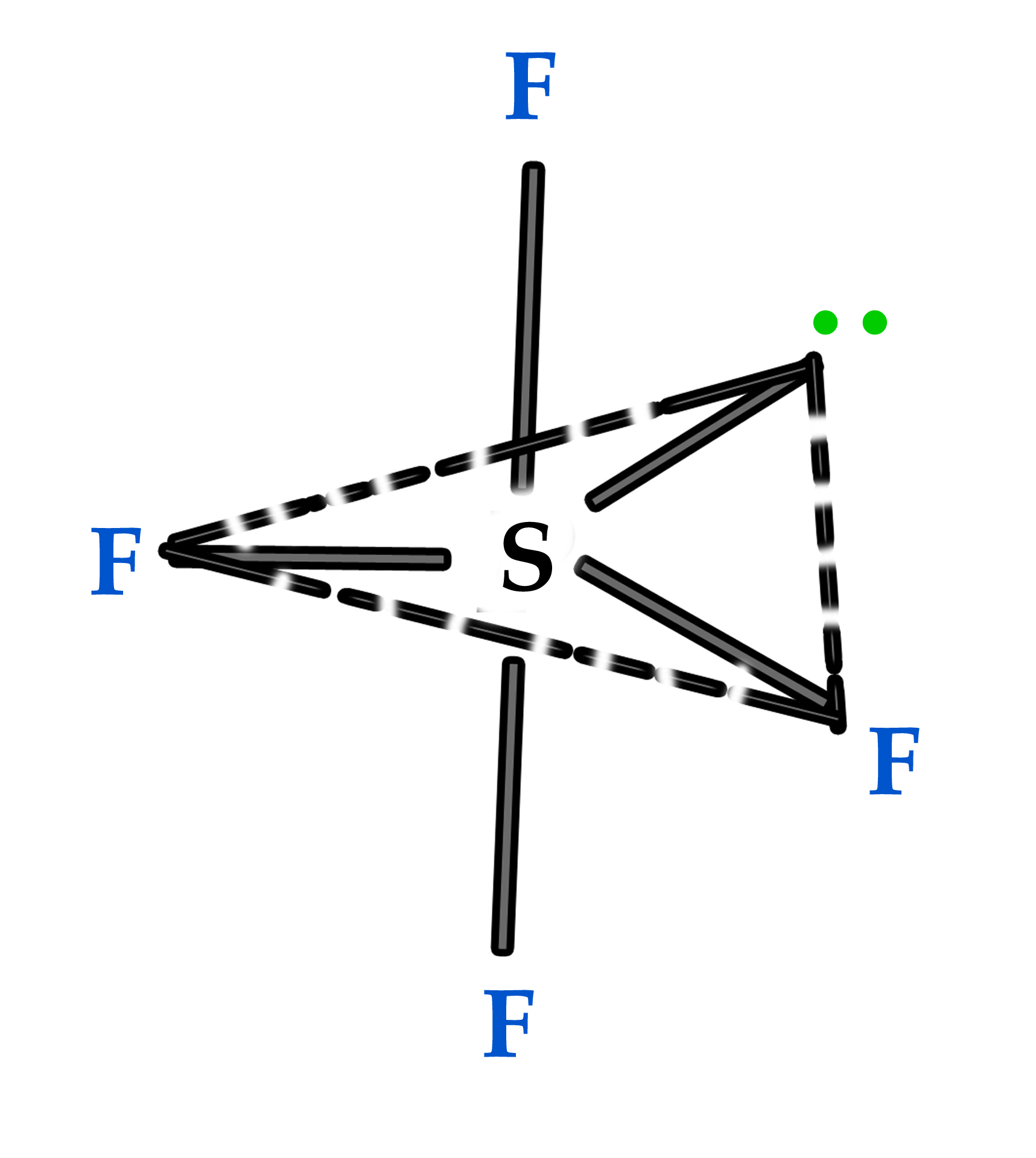
So the correct structure for this compound is  – 

We shall study some more examples of this rule in our next post. Till then, 

Be a perpetual student of life and keep learning …

Good day!