82.Covalent Bonding(28) – MOT(3)- LCAO approximation(1).

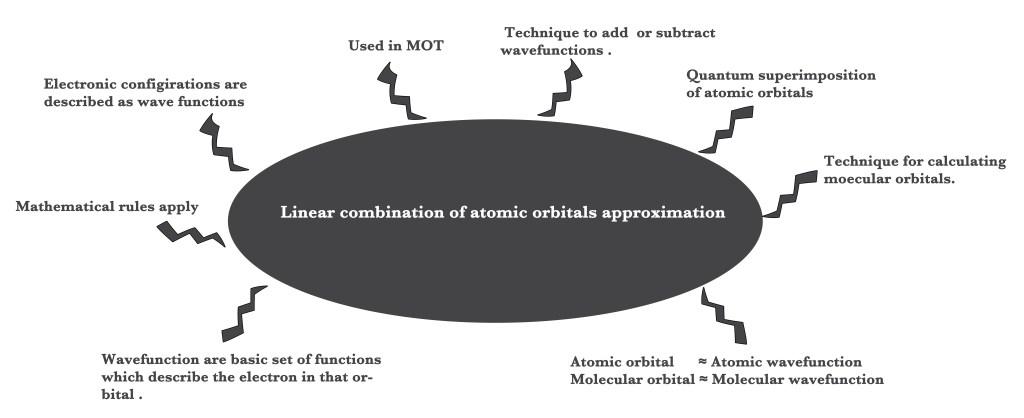
LINEAR COMBINATION OF ATOMIC ORBITALS (LCAO approximation)

Classical physics and quantum mechanics are two very different approaches. Classical physics comprises all the theories that were enunciated before the knowledge of quantum mechanics. These theories are successful in describing everyday observable entities like gravity, electromagnetism, etc. In classical physics, the outcomes of events can be exactly predicted.

However, the MO theory is incorporated in quantum mechanics. Quantum mechanics deals with the microscopic/subatomic world. It measures the possibility of the occurrence of events in probabilities. Thus, exactly predicting a certain outcome is impossible in quantum mechanics. Thus, we need different techniques to describe phenomena and species in the quantum realm.LCAO approximation is one such technique that allows us to combine atomic orbitals together and this technique forms the basis of the application of MO theory to molecules.

 

We already know that, in MOT,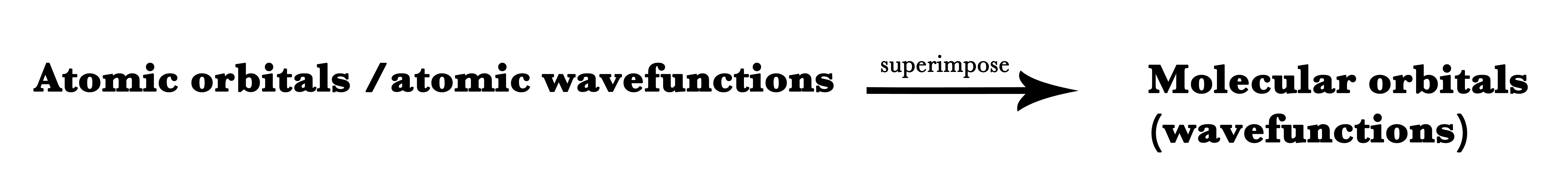

The LCAO  technique is used in quantum mechanics to help in quantum superimposing two atomic orbitals.

Superimposition means to lay one over the other. After two waves superimpose, their wave functions can either add or subtract i.e they can either superimpose constructively or destructively.

Thus, the LCAO  technique is used to construct molecular orbitals by adding or subtracting atomic wave functions. Wave functions are synonymous with orbitals. Thus, this is a technique to add or subtract atomic orbitals to form new molecular orbitals.

Thus, in MOT molecular orbitals are expressed as linear combinations of atomic orbitals. The method used is called the LCAO method.

According to the LCAO approximation,

# of atomic orbitals = # of molecular orbitals.

Let us apply this method to two s- orbitals. Consider two atoms a and b. The following figure shows how the atomic orbitals superimposed to form a bonding molecular orbital,σ_1s.

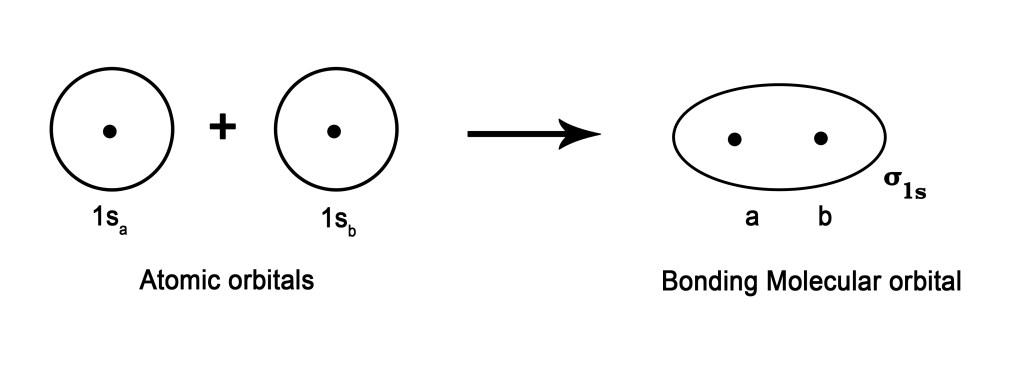
But we know that when two atomic orbitals superimpose, they also form anti-bonding orbitals. So, the above two orbitals will form an ABMO, σ^*_1s –

Have a closer look at both the BMO and ABMO in the above figures. What is the difference between the two?

Bonding MO	Anti Bonding MO
In the BMO, the electron density between the two nuclei is enhanced. Thus, the electrons in this orbital are more stable. This stability is due to the fact that electrons in this orbital get attracted by both the nuclei and also because the nuclear-nuclear repulsion decreases.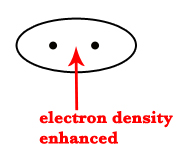	In an ABMO, there is no or very little electron density between two atoms. Thus, the nuclear repulsions are more. This increases the energy of these orbitals.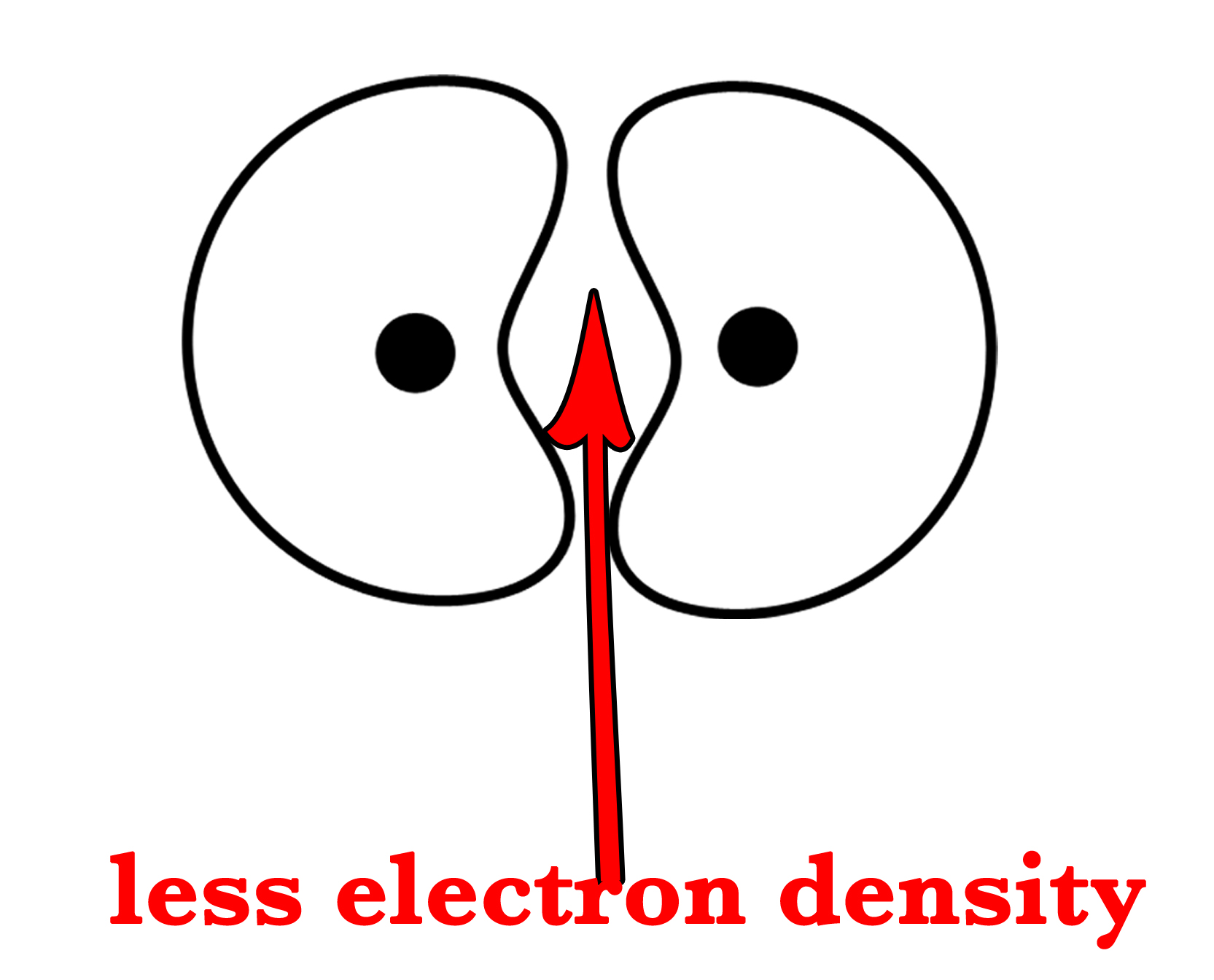

How can we explain the same phenomenon by considering wave functions? We shall learn that in our next post. Till then,

Be a perpetual student of life and keep learning…

Good Day!