119.Frost Musulin diagram/ Polygon Method.

\

This is a very useful mnemonic device for quickly setting down molecular diagrams for cyclic systems. A Frost circle is a simple diagrammatic method used in molecular orbital (MO) theory to predict the relative energies of π molecular orbitals in cyclic, planar, conjugated molecules (like benzene, cyclobutadiene, etc.).

---

According to Hückel’s molecular theory, in cyclic conjugated systems, each carbon contributes a p orbital with one electron (if it has a double bond).

We approximate orbital energies using the formula –

E= α + mβ

where:

α (alpha) → base energy of an isolated carbon p orbital (a reference point).
β (beta) → resonance integral which shows interaction between neighbouring carbon’s p orbitals.
m → a number that tells us how strongly an orbital is stabilised or destabilised compared to the reference energy α. The value of m is obtained by solving the secular determinant, which is a mathematical procedure beyond the scope of our study.
If m< 0 → bonding orbital (stabilised).
If m>0 → antibonding orbital (destabilised).
If m=0 → nonbonding orbital (same energy as α).

Also, β is negative, i.e β < 0, so it lowers energy when orbitals overlap constructively (bonding).
If the overlap is destructive (antibonding), energy goes above α.

(α+β) → a value below α, correctly representing a bonding orbital (as β is negative).
(α−β) → a value above α, representing an antibonding orbital.

---

Rules for drawing frost circles

1. A circle of diameter 4β (radius 2β) is drawn.
2. A regular polygon (all sides are equal) of n sides is inscribed in this circle, with one corner/vertex at the lowest point. n ⇒ # of atoms in the cyclic system.
3. The points at which the corners of the polygon touch the circle, define the energy levels.
4. The horizontal axis (diameter) corresponds to ‘α‘.
5. Below the energy level α all points represent the bonding MOs and above it are antibonding MOs. The points on the diameter are non- bonding.

Let us draw some diagrams to understand this concept better.

---

I] Consider a three-membered ring (n=3). It has two π electrons.

We now inscribe this triangle in a circle, with one vertex down as follows-

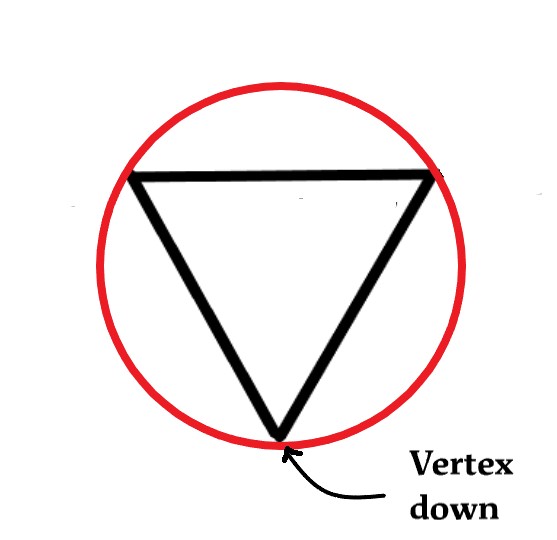
Next, we draw a horizontal line dividing the circle into two halves. The points where the vertices of the triangle meet the circle are the energy levels. The energy levels above the diameter are anti-bonding, and below it are bonding.

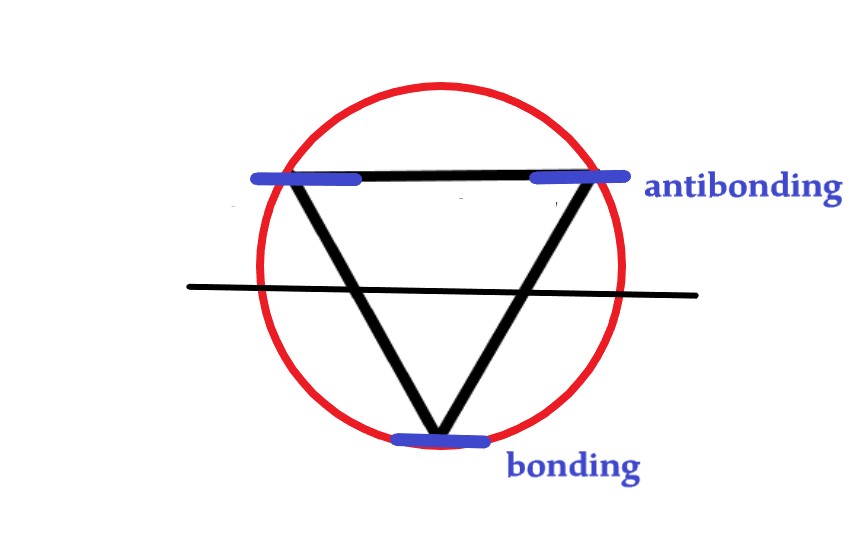
The two electrons will occupy the lowest energy orbital as follows-

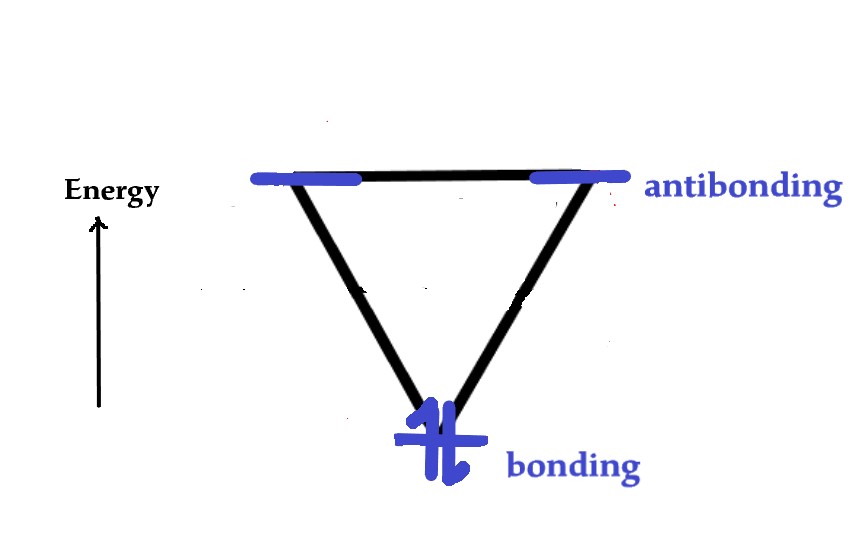
As both electrons are in the bonding MO, the cation is stable and aromatic.

---

II] Consider, 1,3-cyclobutadiene (n=4).

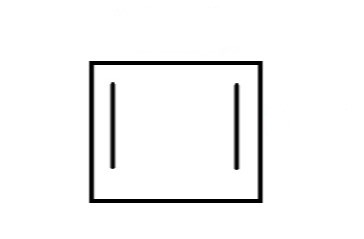
How should the frost diagram look? Can the diagram look like this?

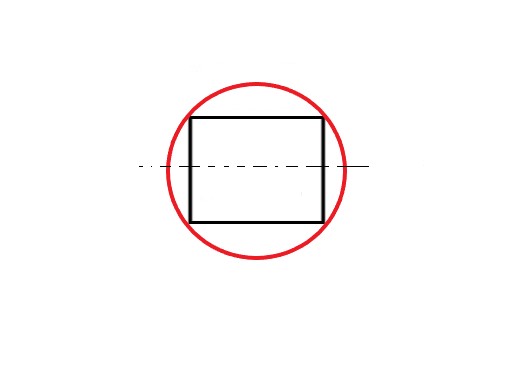
The answer is NO. In the above figure, two vertices instead of one are at the base. So, the correct diagram is –

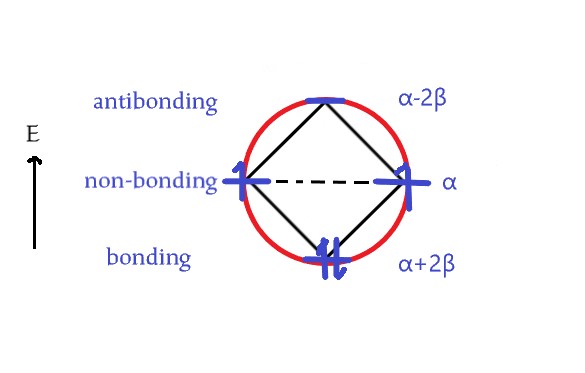
Total energy = 2(α+2β)+2α = 4α+4β.

III] Benzene (n= 6) has six π electrons. It’s frost diagram will look like –

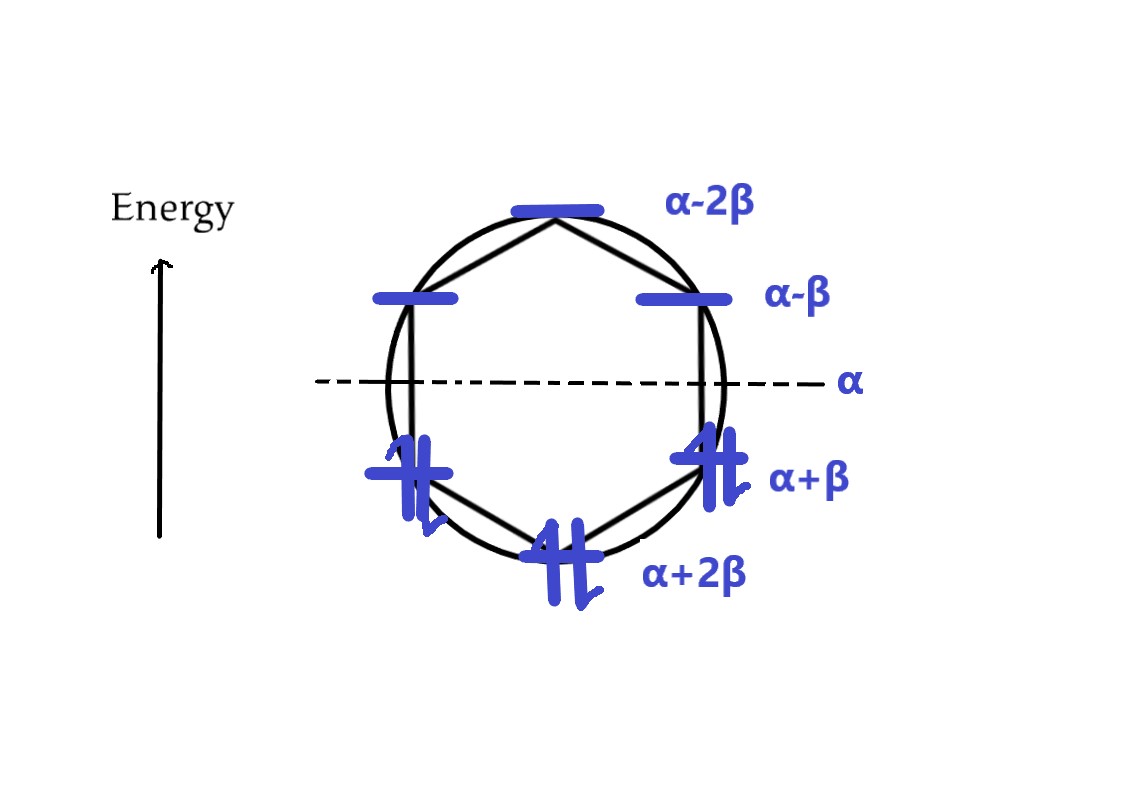
For benzene, the energy levels are – α+2β, α+β, α+β, α−β, α−β, α−2β. There are two electrons in each bonding orbital. Thus,

Total energy = 2(α+2β) + 4(α+β) = 2α + 4β + 4α+ 4β = 6α +8β

As all electrons are in the bonding molecular orbitals, benzene is AROMATIC.

---

In the next post we will compare benzene with cyclobutadiene and see how HMO theory explains their stabilities. Till then ,

Be a perpetual student of life and keep learning….

Good Day !